| De rechte van Euler In een heel oud stoffig meetkund'boek Lees ik over een heel gewone driehoek. Het betreft een doodgewoon figuur, niets bijzonders en niet duur. Kijk, een driehoek met ongelijke zijden. Niets om over uit te wijden. Een driehoek zonder speciale eigenschap. Schijnbaar flauw voor de wetenschap. Eerst gaat het over het punt M. Wat weten we dan van hem? Het is het midden van een kring; door de hoeken loopt het cirkelvormig ding. Dan volgt het zwaartepunt Z, de tweede van de set. 't is mooi: de zwaartelijnen gaan door Z. De zwaart'lijn deelt de overstaande zijde in twee stukken: gelijk van maat zijn beide. Nu dan letterlijk het hoogt'punt H. Dat komt Z en M mooi achterna. Een hoogtelijn snijdt de zij' loodrecht. De hoogtelijnen gaan door H, heus waar, echt ! Maar nu volgt er nog een prachtig wonder. Dat schrijf ik hier graag nog even onder. De punten Z, M en H liggen op één rechte lijn. Dat is het wonder in dit zesd' kwatrijn. Toch zijn we er nog niet. Ik zeg 't maar expliciet: ZM is half zo lang als ZH Da's toch wel heel erg gaaf en prima. De negenpuntscirkel van Feuerbach heeft ook een int'ressant gedrag. Het middelpunt N van dit figuur ligt midden tussen M en H, zeg ik nu met vuur! Tenslotte nog als laatst' mirakel raakt zij d'aangeschreven cirkels buiten de driehoek. En dat is verre van gesneden koek! | Een gedicht, geïnspireerd op: Leerboek der vlakke meetkunde Dr. P. Molenbroek, zevende druk P. Noordhoff N.V., 1931 blz 161, 204, 216 |
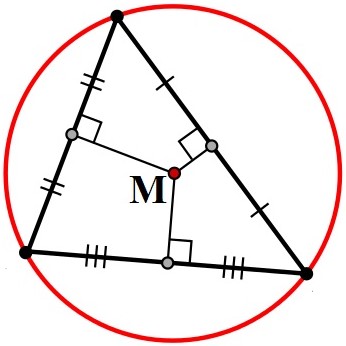 M = middelpunt van de omgeschreven cirkel straal R = abc : √(a+b+c)(-a+b+c)(a-b+c)(a+b-c) | |
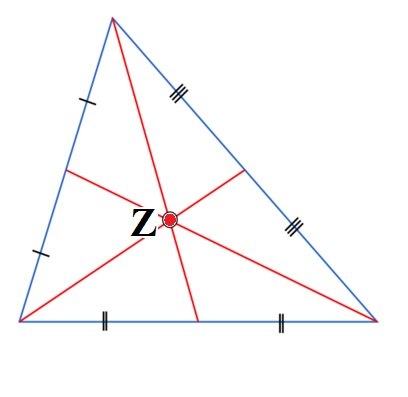 Z = zwaartepunt van een driehoek | |
 H = Hoogtepunt van een driehoek | |
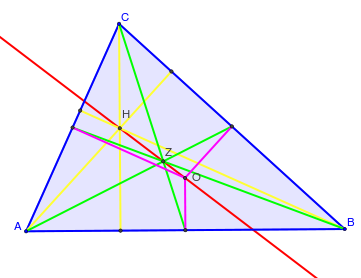 Rechte van Euler De O moet M zijn | |
| |
de middens van de zijden van de driehoek, het snijpunt van de hoogtelijnen met de zijden waarop ze staan, en de middens van de lijnstukken die het hoogtepunt H verbinden met de hoekpunten. | |
en de aangeschreven cirkels uitwendig | |
| Wiskunde | Hoofdmenu |